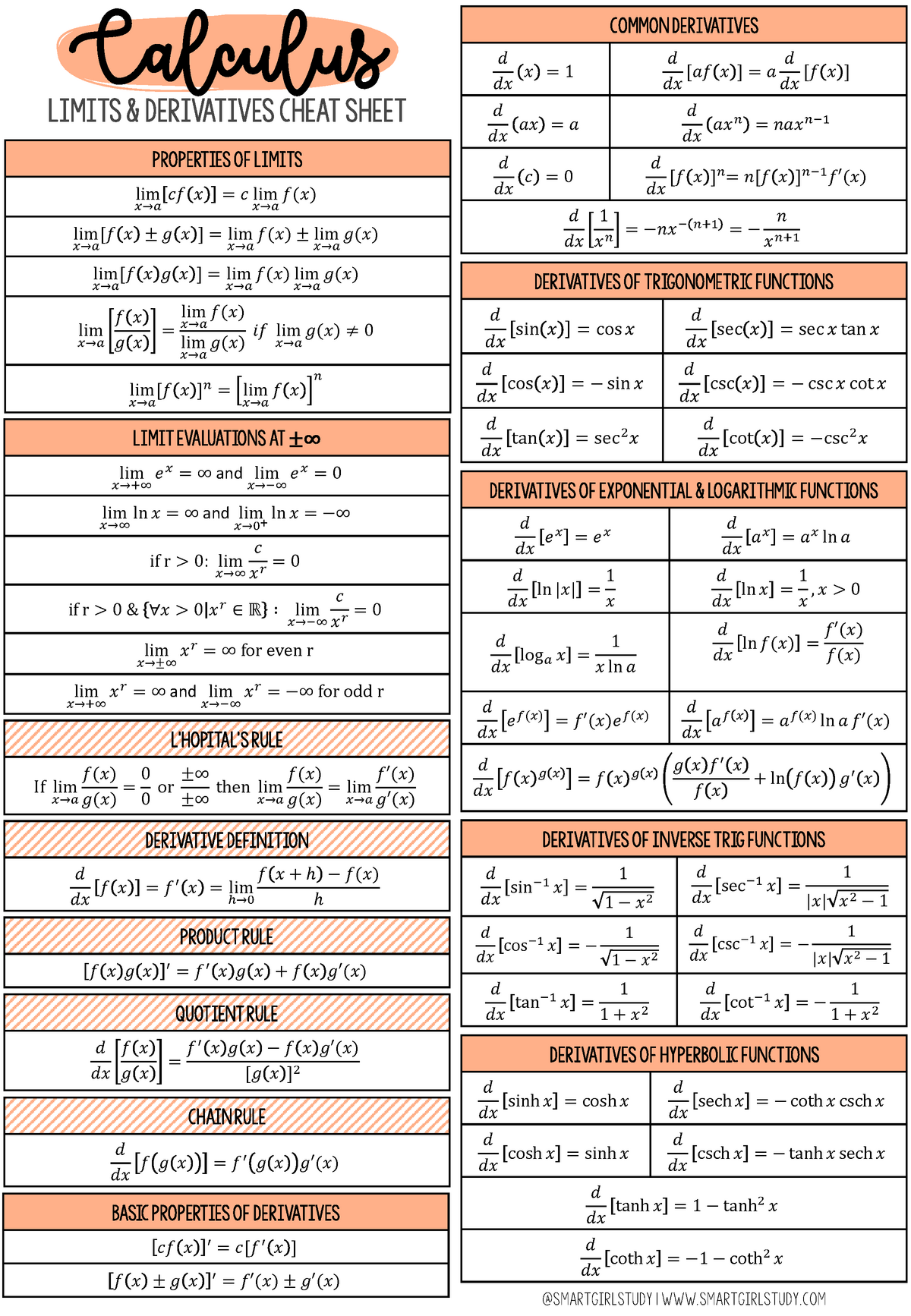
Differentiation Cheat Sheet
Differentiation Cheat Sheet - D dx (xn) = nxn 1 3. D dx (c) = 0; (fg)0 = f0g +fg0 4. Web below is a list of all the derivative rules we went over in class. Determine dimensions that will maximize the enclosed area. Maximize a = xy subject to constraint of. Where c is a constant 2. X + 2 y = 500. F(x) = c then f0(x) = 0. F(x) = xn then f0(x) = nxn−1.
F(x) = xn then f0(x) = nxn−1. Web we’re enclosing a rectangular field with 500 ft of fence material and one side of the field is a building. G(x) = c · f(x) then g0(x) = c · f0(x) power rule: F g 0 = f0g 0fg g2 5. Where c is a constant 2. Determine dimensions that will maximize the enclosed area. X + 2 y = 500. Web derivatives cheat sheet derivative rules 1. Maximize a = xy subject to constraint of. D dx (c) = 0;
F(x) = xn then f0(x) = nxn−1. Web derivatives cheat sheet derivative rules 1. D dx (c) = 0; Determine dimensions that will maximize the enclosed area. Web below is a list of all the derivative rules we went over in class. G(x) = c · f(x) then g0(x) = c · f0(x) power rule: D dx (xn) = nxn 1 3. Maximize a = xy subject to constraint of. Web we’re enclosing a rectangular field with 500 ft of fence material and one side of the field is a building. F(x) = c then f0(x) = 0.
Linear Algebra Cheat Sheet Download Printable Pdf Templateroller Images
Web we’re enclosing a rectangular field with 500 ft of fence material and one side of the field is a building. X + 2 y = 500. Web below is a list of all the derivative rules we went over in class. D dx (c) = 0; F(x) = c then f0(x) = 0.
Differentiation Cheat Sheet Logarithm Derivative
F(x) = c then f0(x) = 0. D dx (c) = 0; D dx (xn) = nxn 1 3. Web below is a list of all the derivative rules we went over in class. (fg)0 = f0g +fg0 4.
Integration and Differentiation Cheat Sheet Cheat Sheet Calculus
F g 0 = f0g 0fg g2 5. Web derivatives cheat sheet derivative rules 1. F(x) = xn then f0(x) = nxn−1. X + 2 y = 500. D dx (xn) = nxn 1 3.
differentiation cheat sheet Google Search Quotient rule
D dx (xn) = nxn 1 3. Web derivatives cheat sheet derivative rules 1. F(x) = c then f0(x) = 0. X + 2 y = 500. (fg)0 = f0g +fg0 4.
Integral cheat sheet Docsity
Web below is a list of all the derivative rules we went over in class. D dx (c) = 0; G(x) = c · f(x) then g0(x) = c · f0(x) power rule: Where c is a constant 2. F(x) = c then f0(x) = 0.
Integration Rules Cheat Sheet
F(x) = xn then f0(x) = nxn−1. Maximize a = xy subject to constraint of. Web we’re enclosing a rectangular field with 500 ft of fence material and one side of the field is a building. G(x) = c · f(x) then g0(x) = c · f0(x) power rule: Where c is a constant 2.
Integration Rules Cheat Sheet
F g 0 = f0g 0fg g2 5. G(x) = c · f(x) then g0(x) = c · f0(x) power rule: Maximize a = xy subject to constraint of. (fg)0 = f0g +fg0 4. D dx (c) = 0;
Calculus Cheat Sheet DIFFERENTIATION FORMULAS Limits & Derivatives
F g 0 = f0g 0fg g2 5. Web below is a list of all the derivative rules we went over in class. D dx (xn) = nxn 1 3. D dx (c) = 0; Where c is a constant 2.
SOLUTION Differentiation cheat sheet 1 Studypool
D dx (c) = 0; Determine dimensions that will maximize the enclosed area. (fg)0 = f0g +fg0 4. Web below is a list of all the derivative rules we went over in class. X + 2 y = 500.
Examples using Implicit Differentiation (solutions, formulas, videos)
Where c is a constant 2. F(x) = c then f0(x) = 0. Web below is a list of all the derivative rules we went over in class. D dx (c) = 0; Maximize a = xy subject to constraint of.
Where C Is A Constant 2.
F g 0 = f0g 0fg g2 5. Web derivatives cheat sheet derivative rules 1. (fg)0 = f0g +fg0 4. Web below is a list of all the derivative rules we went over in class.
Maximize A = Xy Subject To Constraint Of.
F(x) = c then f0(x) = 0. X + 2 y = 500. D dx (xn) = nxn 1 3. Determine dimensions that will maximize the enclosed area.
D Dx (C) = 0;
F(x) = xn then f0(x) = nxn−1. Web we’re enclosing a rectangular field with 500 ft of fence material and one side of the field is a building. G(x) = c · f(x) then g0(x) = c · f0(x) power rule: