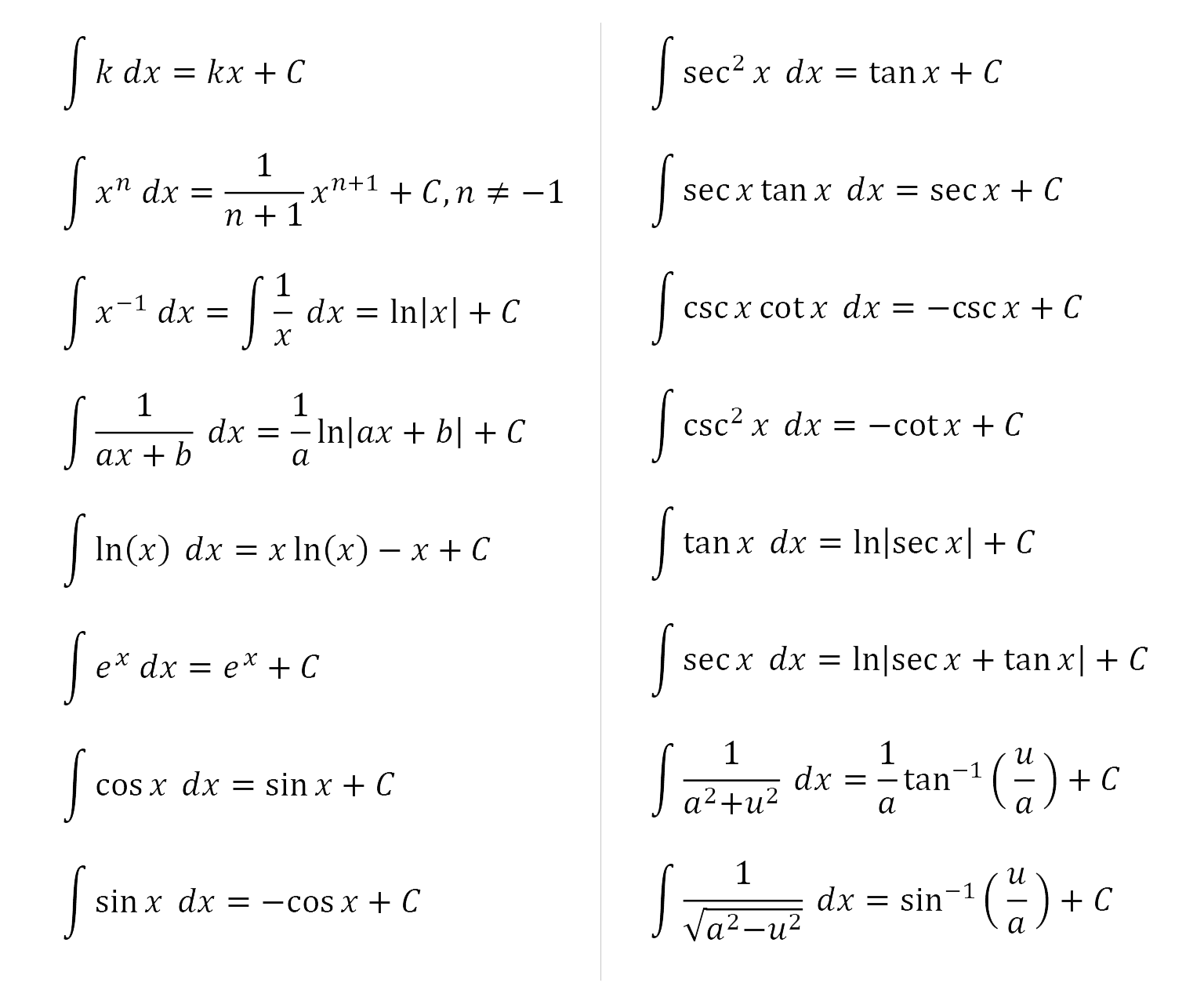Integration Rules Sheet

Integration Rules Sheet - If (𝑥=− (−𝑥), then ∫ (𝑥) 𝑥 − =0 undefined points: The first rule to know is that. Integration can be used to find areas, volumes, central points and many useful things. ∫ f ( g ( x )) g ′ ( x ) dx = ∫ f ( u ) du. If < < , and ( )is undefined, then ∫ (𝑥) 𝑥 = (𝑥 ) 𝑥 =𝐹( )−𝐹( )=lim𝑥→ −𝐹𝑥− lim𝑥→ +𝐹(𝑥) )odd function: ∫ f ( x ) g ′ ( x ) dx = f ( x ) g ( x ) − ∫ g.

∫ f ( x ) g ′ ( x ) dx = f ( x ) g ( x ) − ∫ g. If < < , and ( )is undefined, then ∫ (𝑥) 𝑥 = The first rule to know is that. ∫ f ( g ( x )) g ′ ( x ) dx = ∫ f ( u ) du. If (𝑥=− (−𝑥), then ∫ (𝑥) 𝑥 − =0 undefined points: (𝑥 ) 𝑥 =𝐹( )−𝐹( )=lim𝑥→ −𝐹𝑥− lim𝑥→ +𝐹(𝑥) )odd function: Integration can be used to find areas, volumes, central points and many useful things.

∫ f ( g ( x )) g ′ ( x ) dx = ∫ f ( u ) du. The first rule to know is that. Integration can be used to find areas, volumes, central points and many useful things. If (𝑥=− (−𝑥), then ∫ (𝑥) 𝑥 − =0 undefined points: (𝑥 ) 𝑥 =𝐹( )−𝐹( )=lim𝑥→ −𝐹𝑥− lim𝑥→ +𝐹(𝑥) )odd function: If < < , and ( )is undefined, then ∫ (𝑥) 𝑥 = ∫ f ( x ) g ′ ( x ) dx = f ( x ) g ( x ) − ∫ g.

Basic Integration Rules A Freshman's Guide to Integration

The first rule to know is that. If < < , and ( )is undefined, then ∫ (𝑥) 𝑥 = If (𝑥=− (−𝑥), then ∫ (𝑥) 𝑥 − =0 undefined points: ∫ f ( x ) g ′ ( x ) dx = f ( x ) g ( x ) − ∫ g. ∫ f ( g ( x.

Integration Rules Cheat Sheet

∫ f ( g ( x )) g ′ ( x ) dx = ∫ f ( u ) du. Integration can be used to find areas, volumes, central points and many useful things. If (𝑥=− (−𝑥), then ∫ (𝑥) 𝑥 − =0 undefined points: ∫ f ( x ) g ′ ( x ) dx = f ( x.

Integral cheat sheet Docsity

If (𝑥=− (−𝑥), then ∫ (𝑥) 𝑥 − =0 undefined points: Integration can be used to find areas, volumes, central points and many useful things. ∫ f ( x ) g ′ ( x ) dx = f ( x ) g ( x ) − ∫ g. (𝑥 ) 𝑥 =𝐹( )−𝐹( )=lim𝑥→ −𝐹𝑥− lim𝑥→ +𝐹(𝑥) )odd function: If.

Math for all integration farmula image

∫ f ( g ( x )) g ′ ( x ) dx = ∫ f ( u ) du. If (𝑥=− (−𝑥), then ∫ (𝑥) 𝑥 − =0 undefined points: The first rule to know is that. (𝑥 ) 𝑥 =𝐹( )−𝐹( )=lim𝑥→ −𝐹𝑥− lim𝑥→ +𝐹(𝑥) )odd function: Integration can be used to find areas, volumes, central points and.

Integration Rules, Properties, Formulas and Methods of Integration

(𝑥 ) 𝑥 =𝐹( )−𝐹( )=lim𝑥→ −𝐹𝑥− lim𝑥→ +𝐹(𝑥) )odd function: Integration can be used to find areas, volumes, central points and many useful things. If (𝑥=− (−𝑥), then ∫ (𝑥) 𝑥 − =0 undefined points: If < < , and ( )is undefined, then ∫ (𝑥) 𝑥 = ∫ f ( x ) g ′ ( x ) dx.

Integration Rules and Formulas A Plus Topper

∫ f ( g ( x )) g ′ ( x ) dx = ∫ f ( u ) du. Integration can be used to find areas, volumes, central points and many useful things. If < < , and ( )is undefined, then ∫ (𝑥) 𝑥 = ∫ f ( x ) g ′ ( x ) dx = f.

Integration Rules and Formulas Math formula chart, Math formulas

If < < , and ( )is undefined, then ∫ (𝑥) 𝑥 = Integration can be used to find areas, volumes, central points and many useful things. (𝑥 ) 𝑥 =𝐹( )−𝐹( )=lim𝑥→ −𝐹𝑥− lim𝑥→ +𝐹(𝑥) )odd function: The first rule to know is that. If (𝑥=− (−𝑥), then ∫ (𝑥) 𝑥 − =0 undefined points:

Integration Formulas Trig Definite Integrals Class My XXX Hot Girl

∫ f ( g ( x )) g ′ ( x ) dx = ∫ f ( u ) du. If < < , and ( )is undefined, then ∫ (𝑥) 𝑥 = The first rule to know is that. If (𝑥=− (−𝑥), then ∫ (𝑥) 𝑥 − =0 undefined points: (𝑥 ) 𝑥 =𝐹( )−𝐹( )=lim𝑥→ −𝐹𝑥− lim𝑥→ +𝐹(𝑥).

Integration Rules What are Integration Rules? Examples

The first rule to know is that. ∫ f ( x ) g ′ ( x ) dx = f ( x ) g ( x ) − ∫ g. If < < , and ( )is undefined, then ∫ (𝑥) 𝑥 = (𝑥 ) 𝑥 =𝐹( )−𝐹( )=lim𝑥→ −𝐹𝑥− lim𝑥→ +𝐹(𝑥) )odd function: If (𝑥=− (−𝑥), then ∫ (𝑥).

Integration Rules Integration table Math Original

The first rule to know is that. If (𝑥=− (−𝑥), then ∫ (𝑥) 𝑥 − =0 undefined points: ∫ f ( x ) g ′ ( x ) dx = f ( x ) g ( x ) − ∫ g. If < < , and ( )is undefined, then ∫ (𝑥) 𝑥 = (𝑥 ) 𝑥 =𝐹( )−𝐹( )=lim𝑥→.

Integration Can Be Used To Find Areas, Volumes, Central Points And Many Useful Things.

If (𝑥=− (−𝑥), then ∫ (𝑥) 𝑥 − =0 undefined points: The first rule to know is that. If < < , and ( )is undefined, then ∫ (𝑥) 𝑥 = (𝑥 ) 𝑥 =𝐹( )−𝐹( )=lim𝑥→ −𝐹𝑥− lim𝑥→ +𝐹(𝑥) )odd function: